Series Circuits For Contractor License Exam
A Series Circuit is one in which there is a single electrical-flow path. Below is an example of a series circuits.
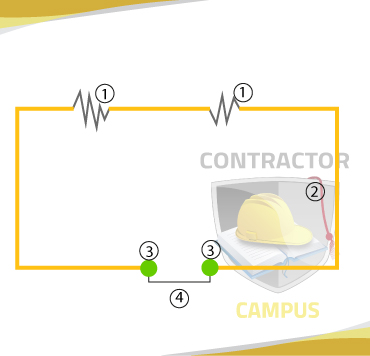
- Resistors: there can be anything from appliances to lightbulbs, anything that consumes electricity and that is connected to the circuit
- Current-flow Path: this is the path through which electricity flows. you can think of this path or being the electrical wine.
- Power source/Switch: this paint at which the circuit connects to the rest of the electrical system or the battery.
- Circuit Status: the line shows whether the circuit is open (off) or closed (on). Think of this line or a bridge, if the bridge connects the two points current will flow.
Notice the circuit above is a series circuit because the current has a single path to flow through. Let's look at more examples.
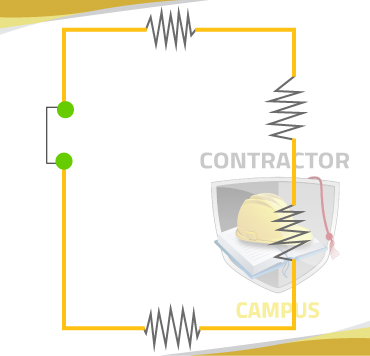

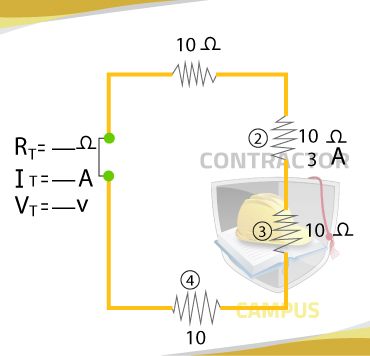
Series Circuit Rules and Formulas
The current at all resistors is the same. The total current for the entire circuit is also the same as that on any resistor.
The total resistance is equal to the sum of the individual resistances.
The total voltage is equal to the sum of the individual voltages.
Example 1: Find the total Voltage, total current, and total Resistance for the series circuit below:
RT = 45 Ω
Since the current is the same everywhere, including the total current for the circuit, the total current must be 3A, the same of the current on resistor 2.
We now have total current and total resistance
Vt = 3A x 45 Ω
Vt = 135V
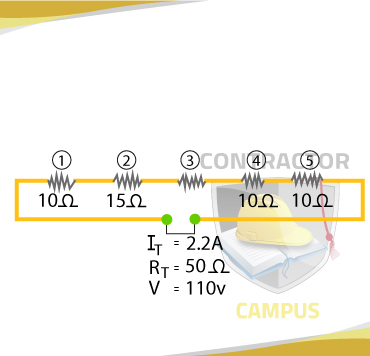
Example 2: What is the resistance on resistor 3?
50 Ω = 10 Ω + 15 Ω + R3 + 10 Ω + 10 Ω
50 Ω - 45 Ω = R3
5 Ω = R3

