Your Cart

Mixed Circuits

A mixed circuit is one in which element flows through a unique path in some areas and through parallel paths in some other areas. Notice on the combination circuit below current flowing through resistor 2 is flowing through a single path, and current flowing through resistor A and B is flowing in parallel.

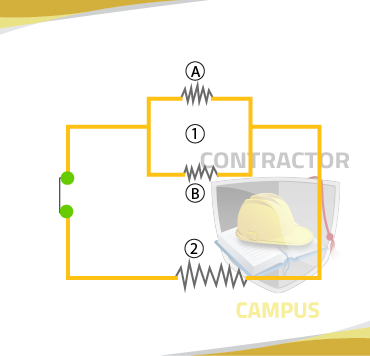
”Mixed_Circuits_2resistors”

To perform calculations on mixed circuits, it is best to think of the circuit or the confirmation of several circuits, some series, and some parallel.

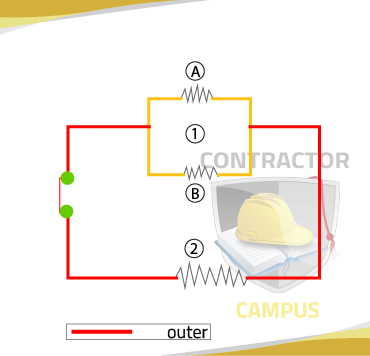
”Mixed_Circuits_outer”
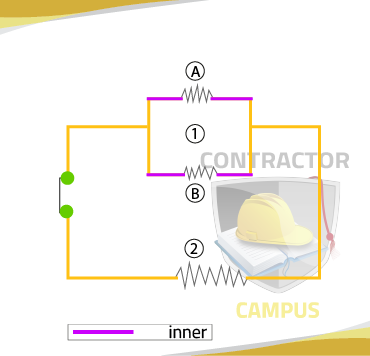
”Mixed_Circuits_inner”

In this particular example, we can think as the outer circuit or as being a series circuit with an "imaginary" resistance 1.
The Voltage, resistance, and current for this "imaginary"? resistance 1 must be obtained from the totals of resistors A and B. We can think of the confirmation of A and B or being the inner circuit. Since A and B are clearly in parallel, parallel rules and formulas must be observed when calculating totals for 1.

Example: Find the total resistance flowing through A and B, the total resistance flowing through C and D, the voltages at A and D, the total resistance for the entire circuit, and the voltage at resistor 1.

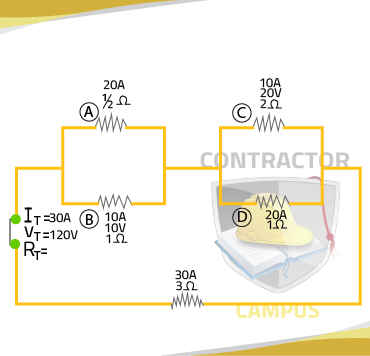
”Mixed_Circuits_Example1”

If you get a problem like this your first step is to "imagine" two resistors which would complete the outer series circuit, of which resistor 1 is part. Calling these imaginary resistors AB and CD in this particular case can be helpful.

Your second step is to label all circuit elements. See image below

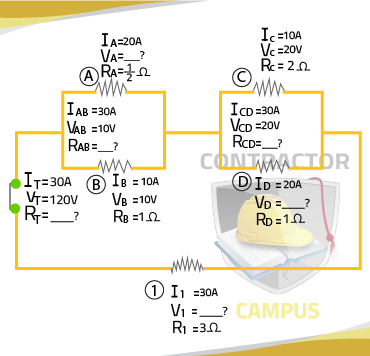
”Mixed_Circuits_2nd_step_label_1”
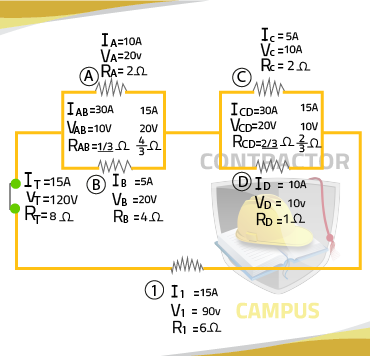
”Mixed_Circuits_answered”

This will allow you to keep track of the information you have, what you are missing and which formulas you can use

  • RAB
    Since A and B are parallel, let's use the following formula.

1/RAB = 1/RA + 1/RB
1/RAB = 1/2 + 1/4

Common denominator is 4.
1/RAB => 1 x 2 / 2 x 2 = 2/4

1/RAB = 2/4 + 1/4 = 3/4
1/RAB = 3 ÷ 3 / 4 ÷ 3 = 1/ 4/3

1/RAB = 1/ 4/3 ; RAB = 4/3 Ω

  • RCD

1/RCD = 1/RC + 1/RD
1/RCD = 1/2 + 1/1

Common denominator is 2.
1/RD => 1 x 2 / 1 x 2 = 2/2

1/RCD = 1/2 + 1/2 = 2/2
1/RCD = 3 ÷ 3 / 2 ÷ 3 = 1/ 2/3

RCD = 2/3 Ω

  • VA
    Since voltage is the same everywhere in a parallel circuit, VA must be the same as VB, therefore VA is 20V.

  • RT
    Since the "outer" circuit is a series circuit, we use the following formula.

RT = R1 + RCD + RAB
RT = 6 Ω + 2/3 Ω + 4/3 Ω
RT = 6 Ω + 6/3 Ω
RT = 6 Ω + 2 Ω
RT = 8 Ω

  • VD
    Since Voltage is the same everywhere in a parallel circuit, VD must be the same as VC, therefore VD is 10V.

  • VI
    Since VI is part of the "outer" following formula:
VT = VI + VAB + VCD
120V = VI + 20V + 10V
120V - 20V - 10V +VI
90V = VI
Details
Written by Yanis O.

Add comment